![]()
Is Superman Fat?December 2012 In the 1978 Superman movie there is a scene where Superman descends on a balcony to visit Lois Lane. In shock, she is struggling to come up with what to say or ask. That leads to a very awkward exchange:
Ok, so there you have it. I don't know if this is a canonical figure, but at least for that movie series we have Superman's physique summarized. So let's run that through a BMI (Body Mass Index) calculation to see how healthy he is. If you don't have one handy, use this one from the National Heart Lung and Blood Institute. You should come up with 27.4, which according to the charts puts him in the middle of overweight, half way to obese. Overweight is 25 to 29.9 Looking at Superman he does not appear to be overweight. So did the script writers make up a bad set of numbers? This is a personal question for me. At the time this movie came out I was a 6 foot 4 teenager, but 165 pounds not 225. That was skinny. I actually knew that 225 was my goal. My older brothers had various Weider exercise equipment and books around the house. Weider gives 225 pounds as the ideal weight for 6 foot 4... and their pictures showed physiques a lot like Superman's. So what's up with the BMI, and why am I putting it in a Physics note? Since growing older I've successfully reached 225 pounds, and exceeded, and gone back and forth a bit. I've never, however, had a physique like Superman. It just isn't distributed the same! In moments of honesty I will admit that even at my "ideal" weight of 225 pounds I look a bit overweight. In that context... a few years ago I came across the Body Mass Index, or BMI when I found that lots of the health advice begins with having me calculate my BMI then advises based on what that says about my percentage of body fat. It would appear that either Superman needs to go on a diet, or this index has some flaws. So I looked up the formula.
On the surface this appears to account for height, but as a physicist one glance at the formula says it must have limited usefulness. We are talking about a volume here. If one uniformly scales any shape its volume grows as the cube of the scaling factor. That is, if you keep all the same fractions of fat to muscle to brain to blood etc, to keep exactly the same body but under different sizes it scales as height^3. Or, 6'4" is 76" -- if you want to know what the weight of somebody 6' (or 72") tall with exactly the same physique as me (at those times when my weight is 225 lbs) it would be:
Now put 6 feet tall and 191.3 pounds into the BMI calculator. You get a body mass index of 25.9. Barely overweight instead of half-way to obese, but for the same physique. So let's push the calculation a bit further, I have prepared the following chart showing the BMI for exactly the same proportions of all aspects of the body given heights from 4 feet to 7 feet using Superman (yellow row) as the reference: 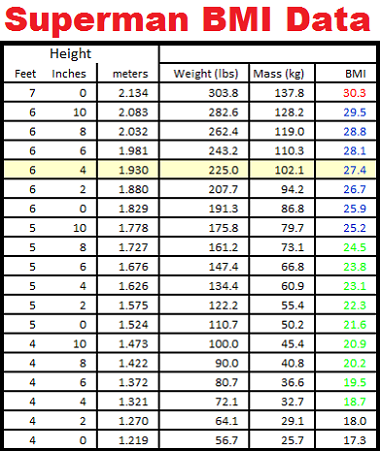
I've also shown the corresponding BMI values in black for underweight, green for normal range, blue for overweight, and red for obese. According to the Wikipedia page on BMI the body mass index was never intended as an individual diagnostic tool. The faults for using it for individuals relate not only to height, but assumptions about ratios of muscle/fat/bone etc. If I am honest I can look at my physique and correctly interpret whether I am an overweight weakling, an athlete carrying a lot of muscle mass, or something in between. I can tell whether my bulges are a point of pride, or incriminating evidence. Without that honest look, how do I know what to think of the BMI? Yet if I do take that honest look, I don't need it. Wikipedia also notes theres is debate about the correct exponent to use with height. The square factor is probably not correct. However, my table above is probably flawed too. That is, the average frame etc. of a tall person is different than that of a short person. They are not, on average, just rescaled duplicates of each other. So a cube factor is probably too big because the assumption that you can just scale with everything is proportion is not generally true either. |