![]()
Music and Physics Notes: Pondering ScalesFebruary 2012 If you take Intro Physics and your Professor plays a musical instrument, you will probably find out during the "Vibrations and Waves" part of the course. I'm among those who would bring a guitar in at some time for the vibrations on a string section. We are realistic enough to know that for many students the top question when they see the guitar will be "is this going to be on the exam?". If the answer is no, you've lost their attention until the guitar goes away. However, we persist because it amuses us and does seem to be appreciated by a few students. I haven't taught at a University for over a decade, so haven't had an audience for the obvious insights and connections that I like to make for a while. Hence, I've decided to open up a new series here where as the mood hits I'll put up some of my standard observations about the connection between Music, Math, and Physics. Today, I'll examine the normal frequencies we hear in our 12 note scale. 12 Notes?Yes, most music that you hear is based on at most 12 notes that make up the standard "chromatic" scale. In fact, it is subsets of this scale, typically about 7 out of the 12 notes, that make up the scales that are typically used. To qualify a bit, after the 12 notes you have completed an "octave" when you get to the 13th note (or the 8th note for 7 note scales like the Major scale - hence the most obvious reason for the word "octave" since "oct" means eight). When you double the frequency of a note, it sounds like the same note, but higher, to our ears. Hence there are many individual octaves of each note that fall within the frequency range that we can hear. Today I'm just going to play with the math a bit to examine the fact that different mathematical ways of deciding what notes fit together commonly comes up with pretty much the same 12 notes. In later articles I'll get more into the Physics, and why if you listen to different instruments you'll find those notes are not exactly the same, and so on. When two different notes sound good together, we call that harmony. The relationship between the frequencies of two notes is called an interval. I've already noted above doubling the frequency, a one octave interval, makes a harmony. This is the most basic harmony - "the same note but higher". An obvious guess is that if the interval 2*frequency is a harmony, so will 3*frequency, 4*frequency, 5*frequency etc. These intervals will generate a pretty small "scale" of harmonizing notes before we run out of the range which we can hear. So, lets try this idea:
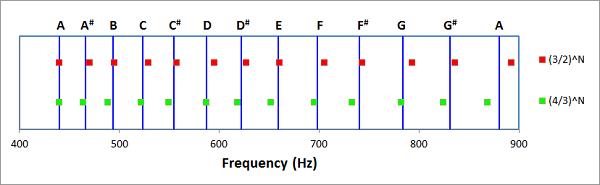
So let's begin with 440 Hz, one octave above being 880 Hz. The next frequency will be 440*3/2 = 660 Hz. After that, 660*3/2 = 990 Hz. This is above 880 Hz, so halve it to get 495 Hz. Continuing like this produces 742.5, 556.88, 835.31, 626.48, 469.86, 704.79, 528.60, 792.89, 594.67, 892.01. This last number is close to one octave (880 Hz), halving it gives 446 Hz - only about 1% higher than where we started. So when will we be exactly one octave? Well, never. We are multiplying by a power of 3 divided by a power of 2. That is an odd number divided by an even number, which cannot be exactly 2. So, lets consider approximately 1% to be close enough and stop there. If the interval frequency*3/2 is a harmony, then so is frequency*2/3 - the reverse step downwards. Double this to get into the same octave and we have a new proposed fundamental interval for harmony, frequency*4/3. We could repeat the game above to get another sequence of numbers. The results of these two methods for generating a "scale" is shown below, with labels of the frequency value shown on the bottom scale and a set of standard note names at the top.
The vertical blue lines show "equal tempering". In this case the interval isn't a fraction but a number chosen such that 12 intervals will exactly double the frequency. This value is 21/12, or approximately 1.059. If the blue lines remind you of the fret spacing on a guitar, there is good reason for that - to be discussed in a later article. Perhaps the most obvious thing about the graphic above is that following an interval rule based on two simple fractions led us to very similar 12-note scales, one a little higher in frequency (higher pitch) than the equally tempered scale, and one a little lower in pitch than the equally tempered scale. This leads to the following speculation:
... continued next month. For now here is a challenge for your ear and to test the idea that "1% is good enough". See if you can hear the difference between these three scales we've defined. The two links below are for the major scale and the chromatic scale, each is played 3 times (one time with each note set shown above). Next month will reveal which scale is which. |