![]()
Music and Physics Notes: Hearing the DifferenceMarch 2012 Last month's note was the first part of a series on Math, Physics, and Music. I began with some simple math ratios to show how repeated applications of frequency*3/2 or 4/3 produced a "scale" of notes similar to what you would get with 12 logarithmically spaced frequencies to double the initial frequency. I ended with a challenge to anyone who wanted to see if they could hear the difference. Here are the links again:
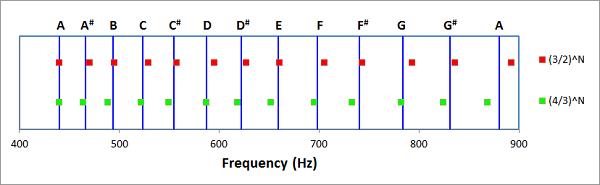
Do Re Mi - the A Major scale Here again is a graphical representation of the three scales you can listen to above:
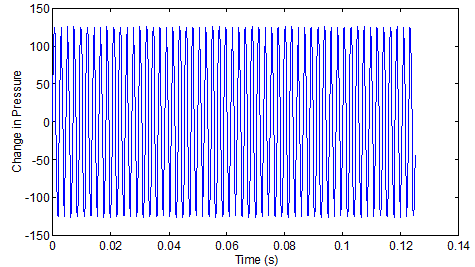
In the graphic it is easy to see the difference. Was it easy to hear the difference? Regardless of how easy or difficult it was to hear that these scales are different, there is is a natural question "what is close enough?", or put a bit differently, "when are two notes so close in frequency that they cannot be distinguished?" To begin to answer that question, let's listen to the three "octaves" without all the in between notes: 440 Hz then 868.156 Hz; 440 Hz then 880 Hz; and 440 Hz then 892.006 Hz. 3 octaves. Was it easier to tell the difference with the in between notes removed? Try this, the three higher "A" notes played after each other without the lower note at all. 868 Hz then 880 Hz then 892 Hz. That should have made it easier still to tell the difference. This should make it easier yet again: 868 Hz then 880 Hz then 892 Hz at uniform volume Before moving on to the next step, playing the notes together, let me explain that last step and a bit more about the Physics of sound and music. What do we man when we say that an "A above middle C" is 440 Hz, and which of the two ways I've played this note is correct? Consider that your ear is at a certain point in space and the pressure of the air is rising and falling by a small amount 440 time per second at that spot. That is the frequency of the vibration (change in pressure) is 440 times per second, or 440 Hz. You will hear the A note and the volume will be louder when the range of the pressure change is higher. I'll return to the shape in more detail in some other month's note. For now what I want to say is that just that frequency is rather dull sounding. Real instruments are characterized in part by the frequencies at which they vibrate the air and in part by the "waveform" of the vibration. In fact, a completely ideal 440 Hz sound would have started infinitely far in the past in end infinitely far in the future. So any real note you hear is some cobination of frequencies wrapped in a waveform. In music the waveform tends to be fairly simple, often characterized by "attack" (the rising in volume to start the note) and "decay" (the falling in volume to end the note). So what we have is two different waveforms wrapping the oscillation. Most of the sound files I've presented were instant on, and an exponential decay. The last one is instant on, uniform for two seconds, then instant off. This is closer to "ideal" perhaps, but the simpler waveform make it easier to hear differences. In case it helps, consider this in pictures. First, here is the rising and falling in pressure at some spot (with 0 being the average air pressure) at 440 Hz, shown for a little more than a 10th of a second:
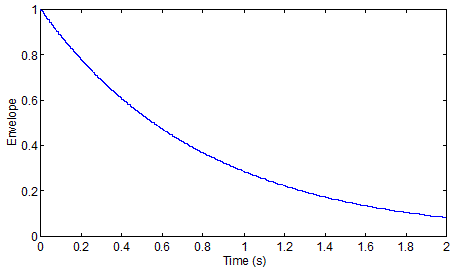
Count the peaks above, you will see that in a tenth of a second there are 44, thus 440 in a full second. Now, here is an exponential decay "waveform" with a decay constant set to bring the size of vibration down a lot in a second or two.
So, at any time multiply the pressure difference in the first 440 Hz soundwave by the value of the decaying waveform. The quarter of a second looks like this.
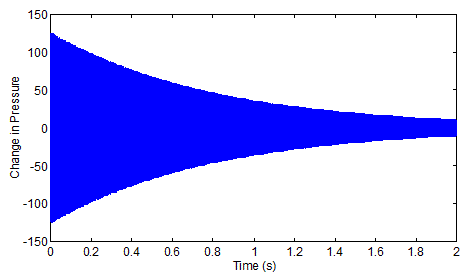
After that, the individual oscillations in pressure get pushed so close together in our graphic that you cannot see them. If we then show a couple of seconds, the main thing you still see is the waveform, but as a symmetric solid object centered around zero.
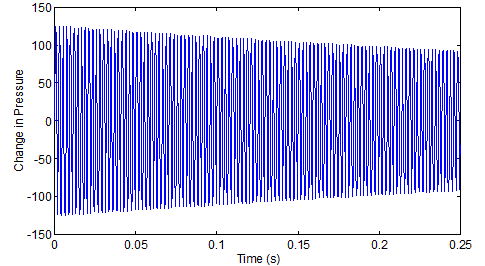
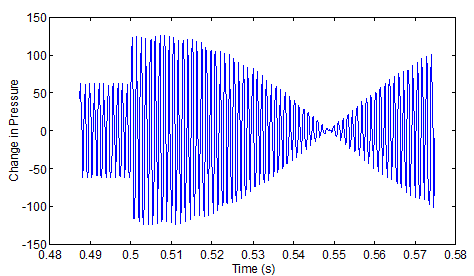
When listening to notes one after the other, of course it will be harder to tell the difference if one has become quiet before the other begins. That brings us to the next consideration, playing the notes together. Try listening to this: half a second of 868 Hz, followed by 2 seconds overlapped with 8800 Hz, followed by half a second of just 880 Hz.Here is what a graph of the vibrations looks like as the transition starts (count the oscilations in one 0.01 s time division, you should get about 9, which multiplies out to about 900 per second).
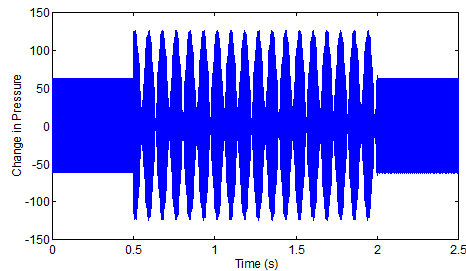
Note that you don't see two vibrations, the total of the two vibrations is a single vibration which is the sum of the two at any given time. There are times where they add together and times when they cancel each other out. Hence the vibration you hear keeps rising and falling in volume. Here is the graph for the total sound file:
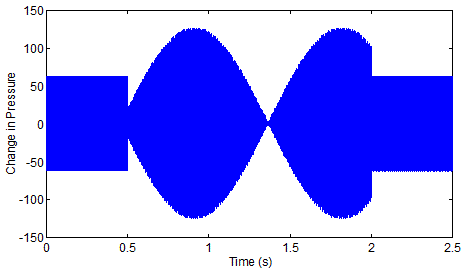
So when you listen two it you probably didn't hear it as two notes. Rather you probably heard it as a single note that rose and fell in volume several times. This is called "beating". These beats are a basic tool used for tuning instruments. Listen to the beats when the two frequencies are so close that you have trouble hearing the difference, Here is one last thing to see and hear for this month: the same test but starting with 878.9 Hz. I was going to do 879 Hz, but I like the appearance of the graph below when I start just a bit differently.
Notice that when the frequencies are much closer the beats come a lot slower. So when tuning an instrument you listen for the beats between notes and make them as far apart as you can. The closer the frequencies are together, the longer the time between beats will be. I'll end this month's note with the observation that we now have a way of predicting when notes are essentially identical no matter how good your ear is - if the beating is longer than the length of the waveform, there isn't time to hear a difference. Hence, if you think your instrument is a bit too much out of tune, play "stacatto" as much as you can get away with... Starting next month we're now in a position to start looking at a whole range of things that come out of what happens when notes play simultaneously - what fractions actually do sound harmonious together? What is their relationship to the even tempered scale? If all I heard was the middle section of the last sound file, would I perceive it as any different than a single note with a certain waveform? ... and more. |