![]()
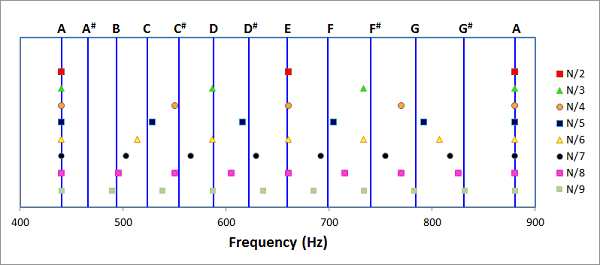
Music and Physics Notes: Fractions and HarmonyApril 2012 Last month's note was the second part of a series on Math, Physics, and Music looking at the question of how close is close enough to consider two notes to be the same. This month I return to the question of what frequency intervals sound harmonious, and why. In the first part of this series I examined the curious fact that multiplying a starting frequency by combinations of 3/2, 4/3 and 1/2 would produce a set of notes quite close to those obtained by increasing frequency 12 times by a factor of 21/12. One curious aspect of this is that one set of frequencies is rational multiples of the starting frequencies, the other irrational. In fact, if factors like 128/81 or 81/64 are deemed a nice harmonic relation to the starting frequency, doesn't it seem that pretty much any fraction will be? To explore a bit further, here is a comparison of the "equal tempered scale" with various fractions.
The red dots are 440 Hz, 440*3/2 Hz and 440*2 Hz.
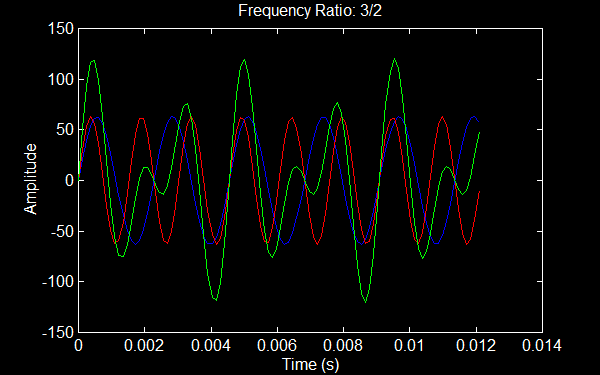
Looking at the above plot I would be hard pressed to make a case that the familiar 12 tone scale can be arrived at by a simple principle of using intervals of arbitrary fractions. A few intervals defined by fractions come quite close to the scale notes. This begs questions such as "are the other fractions not harmonic, or is our normal scale missing a lot of harmonic combinations?" To continue, lets look closer at the case of the interval 3/2. Below 440 Hz is shown in blue, 440*3/2 Hz is shown in green, and the sum of the two is shown in green:
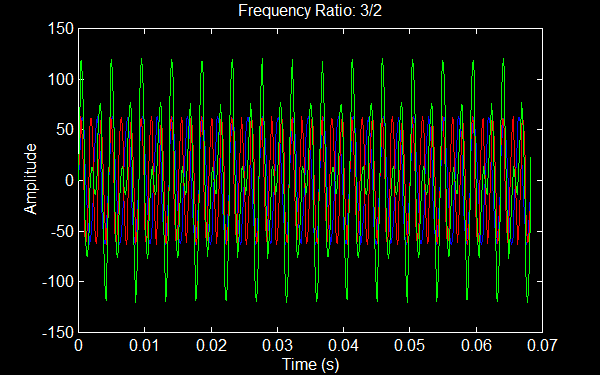
You can see that there is a simple visual pattern to the combination - every 2 cycles of blue and every 3 cycles of green repeats. For example, they cross with an amplitude of zero at approximately 0 s, 0.045 s, 0.09 s, etc. If we show a longer time period the pattern is shown to keep repeating.
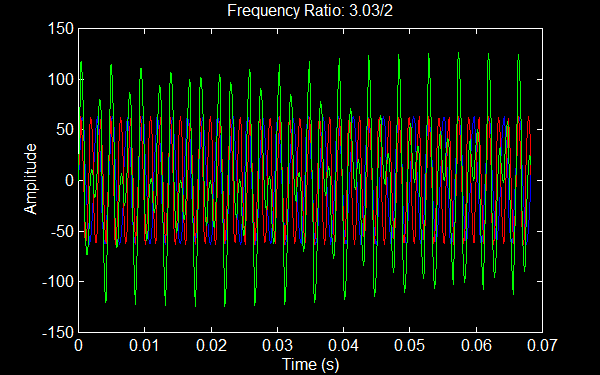
Now take a look at a small (1%) variation in the interval.
This still looks similar, but does not repeat in as simple a fashion. One would wait a much longer time to get a repetion of the pattern. Hence the ingredient that seems to make a harmonic sound is that similarly to single notes there is a reasonably simple repeating pattern. Below are links to listen to the same comparison. In both sound files the two notes are compared one after the other with decay function envelope, then played with a uniform envelope with a period of overlap. I'll leave it for you to make conclusions about the sound, but this is in the range discussed last month where (depending on your ear and how the notes are played) you are near the limit of where you can distinguish notes. I will return to the matter of other frequency intervals (especially other fractions) later. For the next month or two I'm going away from the speculation and math games I've been doing so far to talk about what frequencies commonly exist in the sounds we hear such as from vibrations on a string... If you want some musical amusement in the meantime, try this fun site: Seaquence |